
算法是任何过程中不可或缺的一部分, 因此访问员会问你许多与算法有关的问题。
这是一些最常被问到的算法面试问题及其答案的列表。这些问题对于学术和竞争性考试的观点也是有益的。
1)什么是算法?对算法有何需求?
算法是定义明确的计算过程, 将某些值或一组值作为输入, 并生成一组值或某些值作为输出。
需要算法
该算法提供了该问题的基本思想和解决方法。使用算法的一些原因如下。
- 该算法提高了现有技术的效率。
- 比较其他技术的算法性能。
- 该算法为设计人员提供了对需求和问题目标的强大描述。
- 该算法提供了对程序流程的合理理解。
- 该算法在不同情况下(最佳情况, 最坏情况, 平均情况)测量方法的性能。
- 该算法标识算法所需的资源(输入/输出, 内存)周期。
- 借助算法, 我们可以测量和分析问题的复杂性时间和空间。
- 该算法还降低了设计成本。
2)算法的复杂性是什么?
算法的复杂性是对算法与替代算法的效率进行分类的一种方法。它的重点是执行时间如何随要处理的数据集而增加。该算法的计算复杂度在计算中很重要。
非常适合根据算法所需的相对时间量或相对空间量对算法进行分类, 并根据输入大小来指定时间/空间需求量的增长。
时间复杂度
时间复杂度是程序的运行时间, 它是输入大小的函数。
空间复杂度
空间复杂度基于算法完成任务所需的空间来分析算法。在计算的早期(当计算机上的存储空间有限时), 空间复杂性分析至关重要。
如今, 空间问题很少发生, 因为计算机上的空间足够广泛。
我们实现了以下类型的复杂性分析
最坏情况:f(n)
它由在大小为n的任何实例上执行的最大步骤数定义。
最佳情况:f(n)
它由在大小为n的任何实例上执行的最小步骤数定义。
平均情况:f(n)
它由在大小为n的任何实例上执行的平均步骤数定义。
3)编写算法以反转字符串。例如, 如果我的字符串是” uhsnamiH”, 那么我的结果将是” Himanshu”。
反转字符串的算法。
第一步:开始
第二步:取两个变量i和j
步骤3:做长度(string)-1, 将J设置在最后一个位置
步骤4:执行字符串[0], 将i设置为第一个字符。
步骤5:字符串[i]与字符串[j]互换
步骤6:将i递增1
步骤7:将j递增1
步骤8:如果i> j, 则转到步骤3
步骤9:停止
4)编写一种算法, 以将节点插入到已排序的链表中。
在已排序的链表中插入节点的算法。
情况1:
检查链接列表是否为空, 然后将节点设置为head并返回它。
New_node-> Next= head;
Head=New_node情况2:
在中间插入新节点
While( P!= insert position)
{
P= p-> Next;
}
Store_next=p->Next;
P->Next= New_node;
New_Node->Next = Store_next;情况3:
在最后插入一个节点
While (P->next!= null)
{
P= P->Next;
}
P->Next = New_Node;
New_Node->Next = null;5)什么是渐近符号?
渐进分析用于测量不依赖于机器特定常量的算法的效率, 并阻止该算法比较耗时算法。渐进符号是一种数学工具, 用于表示渐进分析算法的时间复杂度。
三种最常用的渐近符号如下。
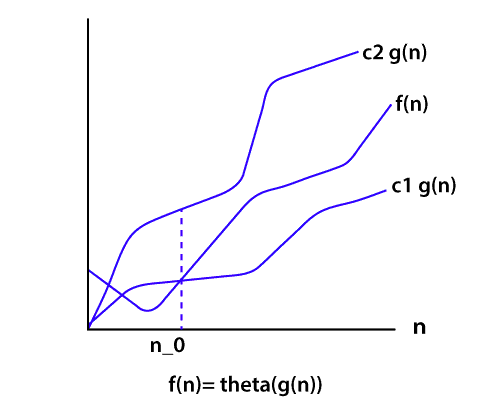
θ符号
θ符号定义确切的渐近行为。要定义行为, 它从上方和下方限制功能。获得表达式Theta表示法的一种便捷方法是删除低阶项并忽略前导常数。
大O符号
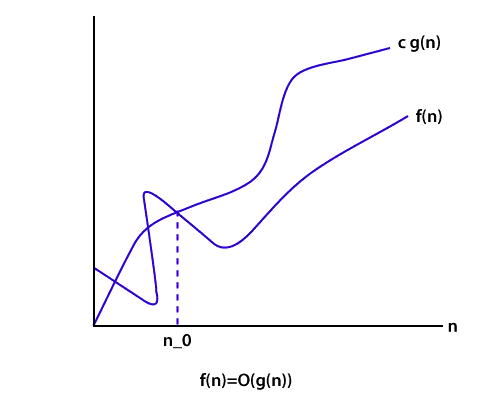
Big O表示法从上方限制函数, 它定义了算法的上限。让我们考虑一下插入排序的情况;在最佳情况下需要线性时间, 在最坏情况下需要二次时间。插入排序的时间复杂度为O(n2)。当我们仅对算法的时间复杂度有上限时, 这很有用。
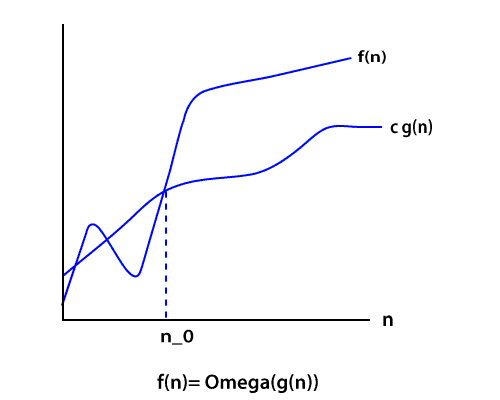
哦记法
就像Big O符号提供渐近上限一样, Ω符号提供函数上的渐近下限。当我们对算法的时间复杂度有较低的限制时, 这很有用。
6)解释冒泡排序算法?
气泡排序是所有排序算法中最简单的排序算法。如果相邻元素顺序错误, 它会通过交换相邻元素来重复工作。
例如
(72538)我们使用此数组进行排序。
1步:
(72538)->(27538)交换7和2。
(27538)->(25738)交换7和5。
(25738)->(25378)交换7和3。
(25378)->(25378)算法不会交换7和8, 因为7 <8。
第2步完成:
(25378)->(25378)算法不会交换2和5, 因为2 <5。
(25378)->(23578)交换3和5。
(23578)->(23578)算法不会交换5和7, 因为5 <7。
(23578)->(23578)算法不会交换7和8, 因为7 <8。
在这里, 排序后的元素是(23578)。
7)如何交换两个整数而不交换Java中的临时变量?
这是一个非常常见的技巧问题。有很多方法可以解决此问题。
但是必要条件是我们必须解决该问题, 而无需交换临时变量。
如果我们考虑整数溢出并考虑其解决方案, 那么它在访问员眼中会给人留下深刻的印象。
假设我们有两个整数I和j, i = 7和j = 8, 那么在不使用第三个变量的情况下如何交换它们。这是期刊问题。
我们需要使用Java编程构造来做到这一点。我们可以通过执行一些数学运算(例如加法, 减法, 乘法和除法)来交换数字。但是也许会产生整数溢出的问题。
使用加减法
a= a + b;
b=a - b; // this will act like (a+b)-b, now b is equal to a.
a=a - b; // (a+b)-a, now, a is equal to b.这是一个很好的把戏。但是在这个技巧中, 如果加法运算大于Integer.MAX_VALUE定义的int原语的最大值, 并且如果减法小于最小值(即Integer.MIN_VALUE), 则整数将溢出。
使用XOR技巧
不使用第三个变量(临时变量)而交换两个整数的另一种解决方案被公认为是最佳解决方案, 因为它也可以像Java示例C, C ++那样以不处理整数溢出的语言工作。 Java支持几种按位运算符。其中之一是XOR(用^表示)。
x=x^y;
y=x^y;
x=x^y;8)什么是哈希表?我们如何使用这种结构来查找字典中的所有字谜?
哈希表是用于将值存储到任意类型的键的数据结构。哈希表由使用哈希函数的数组索引组成。索引用于存储元素。我们使用哈希函数将每个可能的元素分配给存储桶。可以将多个键分配给同一存储桶, 因此所有键和值对都存储在其各自存储桶中的列表中。正确的哈希功能对性能有很大影响。
要在字典中找到所有的七字谜, 我们必须对所有包含相同字母集合的单词进行分组。因此, 如果我们将单词映射到代表其排序字母的字符串, 则可以通过使用其排序字母作为关键字将单词分组到列表中。
FUNCTION find_anagrams(words)
word_groups = HashTable<String, List>
FOR word IN words
word_groups.get_or_default(sort(word), []).push(word)
END FOR
anagrams = List
FOR key, value IN word_groups
anagrams.push(value)
END FOR
RETURN anagrams哈希表包含映射到字符串的列表。对于每个单词, 我们通过适当的键将其添加到列表中, 或者创建一个新列表并将其添加到列表中。
9)什么是分而治之算法?
分而治之不是一种算法;这是算法的一种模式。它的设计方式是:对大量输入进行争议, 将输入分解为小部分, 并为每个小部分确定问题。现在, 将所有分段解决方案合并到全局解决方案中。这种策略称为分而治之。
分而治之使用以下步骤对算法提出争议。
划分:在本节中, 算法将原始问题划分为一组子问题。
征服:在本节中, 该算法分别解决了每个子问题。
合并:在本节中, 该算法将子问题的解决方案组合在一起, 以获得整个问题的解决方案。
10)解释BFS算法?
BFS(宽度优先搜索)是一种图形遍历算法。它开始从根节点遍历图, 并探索所有相邻节点。它选择最近的节点并访问所有未探索的节点。该算法对每个最近的节点遵循相同的过程, 直到达到目标状态为止。
算法
步骤1:设置状态= 1(就绪状态)
步骤2:将起始节点A排队, 并将其状态设置为2, 即(等待状态)
步骤3:重复步骤4和5, 直到队列为空。
步骤4:将节点N出队并进行处理, 并将其状态设置为3, 即(已处理状态)
步骤5:将所有处于就绪状态(状态= 1)的N个邻居排队, 并设置其状态= 2(等待状态)
[停止循环]
步骤6:退出
11)Dijkstra的最短路径算法是什么?
Dijkstra的算法是一种用于在加权图中找到从起始节点到目标节点的最短路径的算法。该算法创建了一个从起始顶点和源顶点到图中所有其他节点的最短路径树。
假设你想以最短的时间从家里到办公室。你知道有些道路非常拥挤, 使用起来很困难, 这意味着这些边缘的重量很大。在Dijkstra的算法中, 该算法找到的最短路径树将尝试避免权重较大的边。
12)举一些分而治之算法的例子吗?
下面列出了一些使用分而治之算法找到其解决方案的问题。
- 进行排序
- 快速排序
- 二元搜寻
- Strassen的矩阵乘法
- 最近对(点)
13)什么是贪婪算法?举个例子吗?
贪婪算法是一种算法策略, 其目的是在每个子阶段为最佳选择而做出, 最终导致全局最优解。这意味着该算法会在不考虑后果的情况下立即选择最佳解决方案。
换句话说, 找到答案时总是采用最佳的即时或局部解决方案的算法。
贪婪算法可以找到一些理想问题的总体理想解决方案, 但对于其他问题的某些实例却可能会发现不理想的解决方案。
以下是使用Greedy算法找到其解决方案的算法列表。
- 旅行商问题
- Prim的最小生成树算法
- Kruskal的最小生成树算法
- Dijkstra的最小生成树算法
- 图形-地图着色
- 图形-顶点覆盖
- 背包问题
- 作业调度问题
14)什么是线性搜索?
线性搜索用于一组项目。它依赖于通过访问途中找到的所有元素的属性从头到尾遍历列表的技术。
例如, 假设一个包含一些整数元素的数组。你应该找到并打印所有元素的位置及其值。在这里, 线性搜索的工作流程类似于用整数将列表的开头到列表的末尾的每个元素匹配, 并且如果条件为” True, 则打印元素的位置”。
实施线性搜索
执行线性搜索需要执行以下步骤。
步骤1:使用for循环遍历数组。
步骤2:在每次迭代中, 将目标值与数组的当前值进行比较
步骤3:如果值匹配, 则返回数组的当前索引
步骤4:如果值不匹配, 请移至下一个数组元素。
步骤5:如果找不到匹配项, 则返回-1
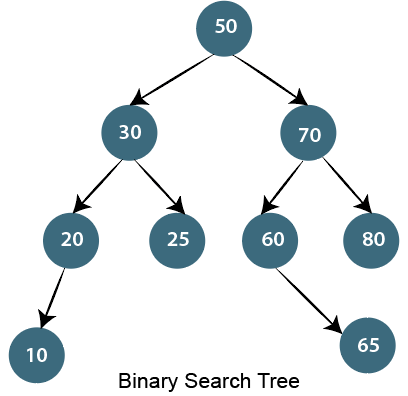
15)什么是二叉搜索树?
二进制搜索树是一种特殊的数据结构, 具有以下属性。
- 小于根的节点将位于左子树中。
- 大于根的节点(即包含更多值)将是正确的子树。
- 二叉搜索树不应有重复的节点。
- 两侧的子树(即左侧和右侧)也应该是二叉搜索树。
16)写一个算法在二叉树中插入一个节点?
插入节点操作是一种平滑操作。你需要将其与根节点进行比较, 并根据要插入的节点的值向左遍历(如果较小)或向右遍历(如果较大)。
算法:
- 将根节点设为当前节点
- 如果要插入的节点<根
- 如果已离开孩子, 则向左走
- 如果没有左子节点, 请在此处插入节点
- 如果要插入的节点>根
- 如果有合适的孩子, 则向右走
- 如果没有合适的子节点, 请在此处插入节点。
17)如何计算二叉树的叶子节点?
算法-
计算叶节点数量的步骤是:
- 如果节点为空(包含空值), 则返回0。
- 如果遇到叶节点。 Left为空, 节点Right为空, 然后返回1。
- 使用以下内容递归计算叶节点的数量
叶节点数=左子树中的叶节点数+右子树中的叶节点数。
18)如何在一个字符板上找到所有可能的单词(Boggle游戏)?
在给定的字典中, 这是在字典和M x N板中进行查找的过程, 其中每个单元格都有一个字符。识别可以由相邻字符的顺序形成的所有可能的单词。考虑到我们可以移动到可用的8个相邻字符中的任何一个, 但是一个单词不应具有同一单元格的多个实例。
例:
dictionary[] = {"Java", "Point", "Quiz"};
Array[][] = {{'J', 'T', 'P', }, {'U', 'A', 'A'}, {'Q', 'S', 'V'}};
isWord(str): returns true if str is present in dictionary
else false.输出
Following words of the dictionary are present
JAVA19)编写算法以在链接列表中插入节点?
算法
- 检查”链接列表”是否没有任何值, 然后将该节点设为head并返回
- 检查要插入的节点的值是否小于头节点的值, 然后在开始处插入该节点并使它成为头。
- 在循环中, 找到要在其后插入输入节点的适当节点。要找到从头开始的正义节点, 请继续转发, 直到到达其值大于输入节点的节点为止。之前的节点是适当的节点。
- 将节点插入在步骤3中找到适当的节点之后。
20)如何删除给定链接列表中的节点?编写算法和程序?
编写函数以从单链列表中删除给定节点。该函数必须遵循以下约束:
- 该函数必须将指向起始节点的指针作为第一个参数, 将要删除的节点作为第二个参数, 即, 指向头节点的指针不是全局的。
- 该函数不应返回指向头节点的指针。
- 该函数不应接受指向头节点的指针。
我们可以假设链接列表永远不会为空。
假设函数名称是delNode()。在直接实现中, 该功能需要在要删除的节点成为第一个节点时调整头指针。
用于删除链表中节点的C程序
我们将处理第一个要删除的节点, 然后将下一个节点的数据复制到head并删除下一个节点的情况。在其他情况下, 当删除的节点不是头节点时, 通常可以通过找到前一个节点来处理。
#include <stdio.h>
#include <stdlib.h>
struct Node
{
int data;
struct Node *next;
};
void delNode(struct Node *head, struct Node *n)
{
if(head == n)
{
if(head->next == NULL)
{
printf("list can't be made empty because there is only one node. ");
return;
}
head->data = head->next->data;
n = head->next;
head->next = head->next->next;
free(n);
return;
}
struct Node *prev = head;
while(prev->next != NULL && prev->next != n)
prev = prev->next;
if(prev->next == NULL)
{
printf("\n This node is not present in List");
return;
}
prev->next = prev->next->next;
free(n);
return;
}
void push(struct Node **head_ref, int new_data)
{
struct Node *new_node =
(struct Node *)malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = *head_ref;
*head_ref = new_node;
}
void printList(struct Node *head)
{
while(head!=NULL)
{
printf("%d ", head->data);
head=head->next;
}
printf("\n");
}
int main()
{
struct Node *head = NULL;
push(&head, 3);
push(&head, 2);
push(&head, 6);
push(&head, 5);
push(&head, 11);
push(&head, 10);
push(&head, 15);
push(&head, 12);
printf("Available Link list: ");
printList(head);
printf("\nDelete node %d: ", head->next->next->data);
delNode(head, head->next->next);
printf("\nUpdated Linked List: ");
printList(head);
/* Let us delete the the first node */
printf("\nDelete first node ");
delNode(head, head);
printf("\nUpdated Linked List: ");
printList(head);
getchar();
return 0;
}输出
Available Link List: 12 15 10 11 5 6 2 3
Delete node 10:
Updated Linked List: 12 15 11 5 6 2 3
Delete first node
Updated Linked list: 15 11 5 6 2 321)编写一个c程序以将链接列表合并到另一个位置?
我们有两个链接列表, 将第二个列表的节点插入第一个列表的第一个列表的替换位置。
例子
如果第一个列表是1-> 2-> 3, 第二个列表是12-> 10-> 2-> 4-> 6, 则第一个列表应变为1-> 12-> 2-> 10-> 17-> 3- > 2-> 4-> 6, 第二个列表应为空。仅在有可用位置时才插入第二个列表的节点。
不允许使用多余的空间, 即必须在一个地方插入。可预测的时间复杂度为O(n), 其中n是第一列表中的节点数。
#include <stdio.h>
#include <stdlib.h>
struct Node
{
int data;
struct Node *next;
};
void push(struct Node ** head_ref, int new_data)
{
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void printList(struct Node *head)
{
struct Node *temp = head;
while (temp != NULL)
{
printf("%d ", temp->data);
temp = temp->next;
}
printf("\n");
}
void merge(struct Node *p, struct Node **q)
{
struct Node *p_curr = p, *q_curr = *q;
struct Node *p_next, *q_next;
while (p_curr != NULL && q_curr != NULL)
{
p_next = p_curr->next;
q_next = q_curr->next;
q_curr->next = p_next;
p_curr->next = q_curr;
p_curr = p_next;
q_curr = q_next;
}
*q = q_curr;
}
int main()
{
struct Node *p = NULL, *q = NULL;
push(&p, 3);
push(&p, 2);
push(&p, 1);
printf("I Linked List:\n");
printList(p);
push(&q, 8);
push(&q, 7);
push(&q, 6);
push(&q, 5);
push(&q, 4);
printf("II Linked List:\n");
printList(q);
merge(p, &q);
printf("Updated I Linked List:\n");
printList(p);
printf("Updated II Linked List:\n");
printList(q);
getchar();
return 0;
}输出
I Linked List:
1 2 3
II Linked List:
4 5 6 7 8
Updated I Linked List:
1 4 2 5 3 6
Updated II Linked List:
7 822)解释加密算法如何工作?
加密是将纯文本转换为秘密代码格式的技术, 也称为”密文”。为了转换文本, 该算法使用一串称为”键”的位进行计算。密钥越大, 潜在的加密模式数量越多。大多数算法使用固定长度为64到128位的固定输入块代码, 而有些算法使用流方法进行加密。
23)算法分析的标准是什么?
通常通过两个因素来分析算法。
- 时间复杂度
- 空间复杂度
时间复杂度是根据一组代码或算法来处理或运行的时间量的量化, 该时间量是输入量的函数。换句话说, 时间复杂度是效率或程序功能处理给定输入所花费的时间。
空间复杂度是算法用于执行和产生结果的内存量。
24)stack和Queue有什么区别?
Stack和Queue都是用于存储数据元素的非原始数据结构, 并且基于某些实际的等效项。
让我们看一下基于以下参数的主要区别。
工作准则
堆栈和队列之间的显着区别是, 堆栈使用LIFO(后进先出)方法访问和添加数据元素, 而队列使用FIFO(先进先出)方法获取数据成员。
结构体
在Stack中, 同一端用于存储和删除元素, 但在Queue中, 一端用于插入, 即后端, 另一端用于元素删除。
使用的指针数
堆栈使用一个指针, 而队列使用两个指针(在简单情况下)。
执行的操作
堆栈用作推入和弹出, 而队列用作入队和出队。
变体
堆栈没有变体, 而队列具有变体, 例如循环队列, 优先级队列, 双头队列。
实作
堆栈比较简单, 而Queue比较复杂。
25)单链表和双链表数据结构有什么区别?
这是关于数据结构的传统面试问题。单链列表和双链列表之间的主要区别在于遍历的能力。
你不能在单链列表中向后移动, 因为其中一个节点仅指向下一个节点, 而没有指向上一个节点的指针。
另一方面, 双向链表允许你在任何链表中双向导航, 因为它维护着指向下一个和上一个节点的两个指针。
| 工作/人力资源面试问题 |
| jQuery面试问题 |
| Java OOP面试问题 |
| JSP面试问题 |
| 休眠面试问题 |
| SQL面试题 |
| Android面试题 |
| MySQL面试问题 |
面试技巧
JavaScript面试问题
Java基础面试问题
Servlet面试问题
春季面试问题
PL / SQL面试问题
Oracle面试问题
SQL Server面试问题
 srcmini
srcmini
评论前必须登录!
注册