JavaScript二叉树实现和原理完全讲解

数组、链表、栈和队列都是线性数据结构，树（tree）是有层次的数据结构，树是非线性数据结构，本质上属于图（graph）（更多图深入的内容可查看：图论算法实现和原理解析）。二叉树的查找效率介于线性表和散列表之间，是比较适中的数据结构，二叉树的查找、插入和删除平均时间都是O(logn)，数据库如MySQL也是使用树实现的（更全面的树内容可查看：二叉树、AVL平衡二叉树、伸展树、B-树和B+树详解）。

一、二叉树的基本概念

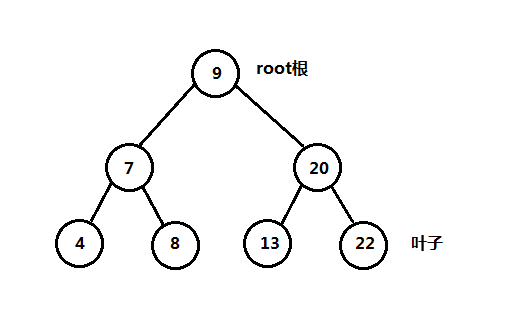
如上图是一个二叉树，最顶部的结点叫做的根，每个结点下面的两个直接几点叫做这个结点的儿子，结点上面连接的是它的父结点。例如根结点9的左儿子是7，右儿子是20，结点8的父结点是7，没有儿子的结点叫做叶子结点，如13是叶子结点。

为什么使用树这种数据结构呢？当遇到需要储存某些有层次的数据信息时，使用树储存更方便，例如计算机内的文件系统。树如二叉树提供更稳定的访问或查找、插入和删除，相对于链表更快（但是比数组和散列表慢），类似于链表，但不像数组，结点间的连接使用指针，可动态创建节点或释放结点。

树或二叉树有哪些应用？可操作有层次或分层的数据；更容易更快访问数据；数据可排序；作为一个工作流程，合成数字图像的视觉效果；路由算法；多阶段决策的多种形式（如决策树）等。

二叉树：一个树中每个结点只有最多两个儿子的树叫做二叉树（binary tree），因为每个结点只有两个儿子，所以我们可以简单地称它们为左儿子和右儿子。

二叉树的结点关键字及其关系：每个结点都有一个关键字key，一般形式是当前结点P关键字P.key大于左儿子的关键字L.key，小于右儿子的关键字R.key。

二叉树的深度和高度：一个结点的深度是指从根结点到该结点的结点数，如上图，结点7的深度为2；一个结点的高度是指从该结点到叶结点的结点数，如结点7的高度为2；一棵树的深度等于它的高度，上图二叉树的高度和深度为3（有些书中，根结点的深度和叶子结点的高度为0，如果使用这个标准，那么相关的操作需要做相应的变化）。

二叉树的数据结构表示：一个树可以用一个根结点的指针root表示，如果树为空，那么root的值为null，一个树结点至少包含以下三个部分：

1. 数据部分
2. 指向左儿子的指针或引用
3. 指向右儿子的指针或引用

二、二叉树的属性详解

二叉树的一些重要属性如下：

1、二叉树中，层次数为l的二叉树的最大结点数为2^(l-1)

其中层数l是根结点到当前结点的结点数，根结点的层数为1，当只有一个根结点事，结点数为2^0=1。因为二叉树只有最多两个儿子，所以在层数l的下一层的结点数有2倍多的结点，即2*2^(l-1)。

2、高度为h的二叉树最大结点数为2^h-1

单结点树的高度为1，上图二叉树的高度为3，最大结点数为2^3-1=7。

3、n个结点的二叉树中，最小可能高度为Log(n+1)，该结论可以由上面的结论推出来。

三、JavaScript实现二叉树

实现二叉树的最重要的两个操作是插入和删除，其中涉及到DFS深度遍历，可查看上面提供的二叉树文章获取更多内容。其中删除操作稍微困难，它的基本逻辑是：

1. 如果只有一个儿子，则使用这个儿子替换当前结点。
2. 如果有两个儿子，获取左子树中的最大值结点q，或右子树的最小值结点q替换该结点，然后再删除q。
3. 对于没有儿子的结点，即叶结点，直接删除。

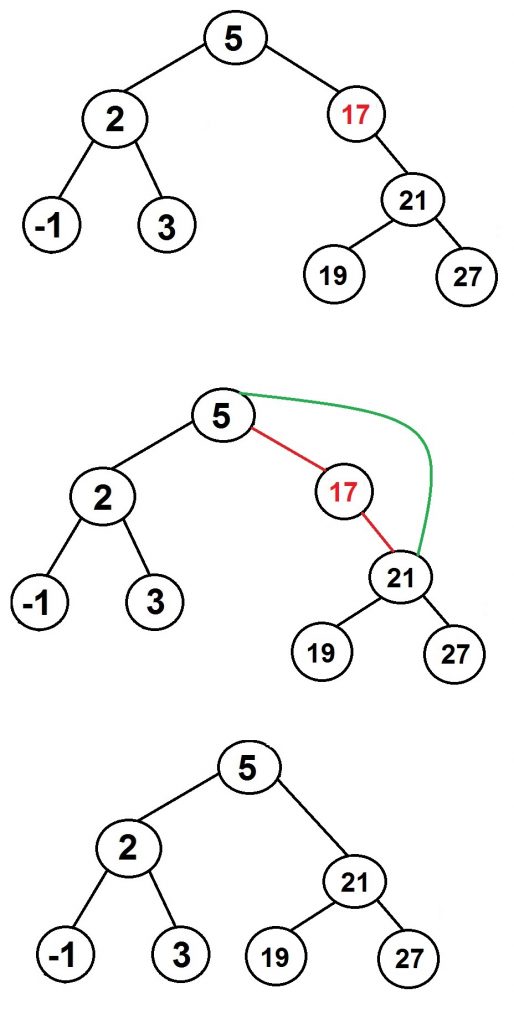
如上图，删除结点17，该结点只有一个儿子21，直接使用21替换17。如果要删除5，因为结点5的关键字比所有左子树的关键字都大，比右子树的所有结点关键字都小，所以，可以取左子树的最大值3替换5，或取右子树的最小值19替换5。

你可以发现，频繁的删除操作会导致二叉树偏左或偏右，导致二叉树极度不平衡，这样会使二叉树的深度过深，最差的情况为O(n)。因此有两种树可以做平衡操作：AVL平衡二叉树和伸展树，更多内容可以参考上面的文章。

二叉树的大部分操作都是基于DFS或BFS，所以如果你对DFS和BFS不了解，建议你参考上面提供的关于树的文章。

下面是普通二叉树的JavaScript实现代码：

// 结点
function Node(key, value){
    this.key = key;
    this.value = value;
    this.left = this.right = null;
}

// 二叉树
function BinaryTree(){
    this.size = 0;
    this.root = null;
}

// 检查二叉树是否为空
BinaryTree.prototype.isEmpty = function(){
    return this.size == 0;
}

// DFS
BinaryTree.prototype.__addNode = function(node, newNode){
    if(node == null)
        return newNode;
    else if(node.key > newNode.key){
        node.left = this.__addNode(node.left, newNode);
        return node;
    }
    else{
        node.right = this.__addNode(node.right, newNode);
        return node;
    }
}

// 添加数据到二叉树中
BinaryTree.prototype.add = function(key, value){
    var node = new Node(key, value);
    this.root = this.__addNode(this.root, node);
    this.size++;
}

BinaryTree.prototype.__findLeftMax = function(node){
    if(node.right == null)
        return node;
    return this.__findLeftMax(node.right);
}

// DFS
BinaryTree.prototype.__deleteNode = function(node, key){
    if(node == null)
        return null;
    if(node.key == key){
        var left = node.left;
        var right = node.right;
        this.size--;
        // 叶子
        if(left == null && right == null){
            return null;
        }
        // 有两个儿子
        else if(left != null && right != null){
            var t = this.__findLeftMax(node.left);
            node.key = t.key;
            node.value = t.value;
            node.left = this.__deleteNode(node.left, t.key);
            return node;
        }
        // 只有一个儿子
        else if(left != null || right != null){
            var t = left != null ? left : right;
            return t;
        }
    }
    else if(node.key > key){
        node.left = this.__deleteNode(node.left, key);
        return node;
    }
    else{
        node.right = this.__deleteNode(node.right, key);
        return node;
    }
}

// 从二叉树中删除一个数据
BinaryTree.prototype.delete = function(key){
    if(this.isEmpty())
        return;
    this.root = this.__deleteNode(this.root, key);
}

BinaryTree.prototype.__search = function(node, key){
    if(node == null)
        return null;
    if(node.key == key)
        return node.value;
    else if(node.key > key)
        return this.__search(node.left, key);
    else
        return this.__search(node.right, key);
}

// 根据key搜索二叉树
BinaryTree.prototype.search = function(key){
    if(this.isEmpty())
        return null;
    return this.__search(this.root, key);
}

// 检查二叉树是否存在某个key的数据
BinaryTree.prototype.contains = function(key){
    return this.search(key) != null;
}

BinaryTree.prototype.__traverse = function(node){
    if(node == null)
        return "";
    var s1 = this.__traverse(node.left);
    var str = s1 + " " + node.key;
    var s2 = this.__traverse(node.right);
    return str + " " + s2;
}

// 遍历二叉树
BinaryTree.prototype.traverse = function(){
    if(this.isEmpty())
        return;
    var str = this.__traverse(this.root);
    console.log(str);
}

// 调用实例
var tree = new BinaryTree();
tree.add(10, 10);
tree.add(6, 6);
tree.add(4, 4);
tree.add(7, 7);
tree.add(20, 20);
tree.add(14, 14);
tree.add(23, 23);
tree.add(15, 15);
tree.add(21, 21);
tree.add(8, 8);
tree.traverse();
console.log("tree contains 20: " + tree.contains(20));
tree.delete(10); // 删除根结点，有两个儿子
console.log("tree contains 10: " + tree.contains(10));
tree.traverse();
tree.delete(15); // 删除叶子结点，无儿子
tree.traverse();
tree.delete(23); // 删除内部结点，只有一个儿子
tree.traverse();